---

last modified: 2024-04-04

---

Hugoniot

• what is shockwave?

  • A disturbance is propagated through the fluid somewhat faster than the speed of sound. Because the disturbance propagates supersonically, it is a shock wave
  • The bulk transfer of kinetic energy heats the post-shock flow. Because the mean free path length is assumed to be negligible in comparison to all other length scales in a hydrodynamic treatment, the shock front is essentially a hydrodynamic discontinuity.
  • In the context provided, the term “discontinuity” refers to a sudden change or break in the physical properties of the fluid flow. Specifically, it refers to the abrupt transition or discontinuous variation in certain parameters (such as density, pressure, velocity, temperature, etc.) across the shock front.
  • In hydrodynamics, shocks are characterized by rapid changes in these parameters over very short distances. When a shock wave passes through a medium, it compresses and heats the material, leading to abrupt changes in its physical properties.

• shock-compression process

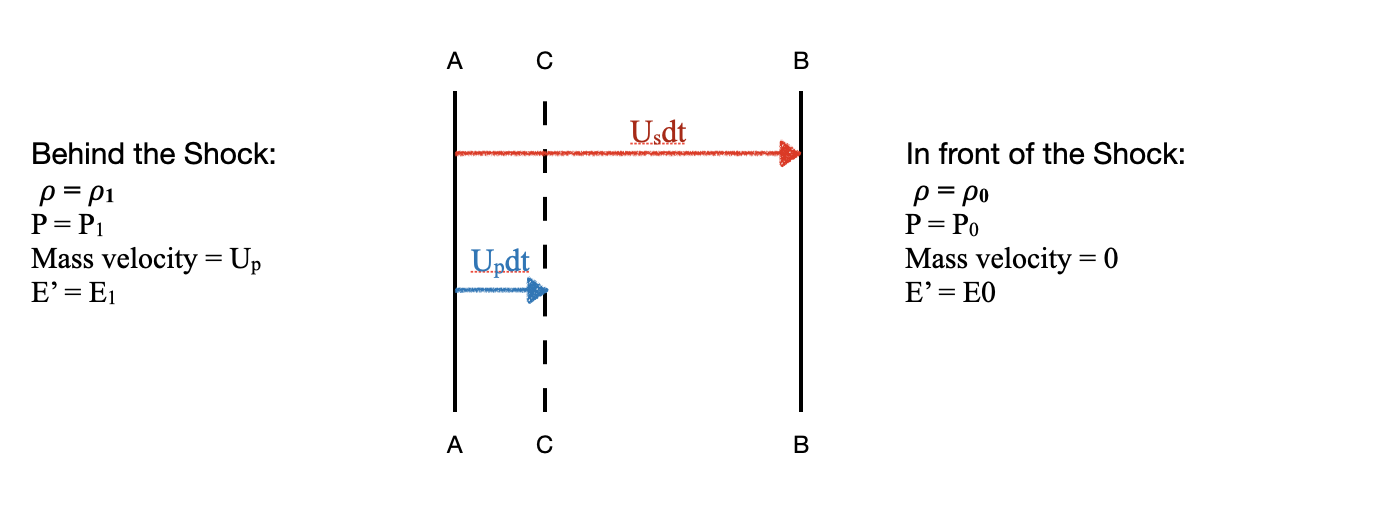
  • Consider a uniform pressure P1 suddenly applied at one face of a plate made of compressible material. Assume that the lateral dimensions of the plate are so large in comparison to the dimension in which the disturbance travels that, for all practical purposes, we may consider them to be semi-infinite. Another way of putting it is that we will learn all that we need to learn about material behavior before the arrival of lateral release waves destroys our condition of uniaxial strain.
  • Assume that the material is initially at a pressure Po. The pressure pulse propagates at a velocity Us. Application of P1 compresses the material to a new density ${\rho }_1$ and at the same time accelerates the compressed material to a velocity Up. Now consider a segment of the material (with unit cross-sectional area) normal to the direction of travel.
  • The position of the shock front at some instant of time is indicated in Fig below by the line AA. Some short interval of time (dt) later, the shock front has advanced to BB while the matter initially at AA has moved to CC. Across the shock front, mass, momentum and energy are conserved.
  

  • conversation of mass

    • conversation of mass across the shock front may be expressed by noting that the mass of material encompassed by the shock wave ${\rho }_0{U}_{s}dt$ now occupies the volume $(U_s-u_p)dt$ at a density ${\rho }_1$
    • ${\rho }_0{U}_s={\rho }_1(U_s-u_p)$
    • Alternatively, in terms of the specific volume $V=1/\rho$
    • $V_1{U}_s=V_0(U_s-u_p)$

  • conversation of momentum

    • is expressed by noting that the rate of change of momentum of a mass of material ${\rho }_0{U}_{s}dt$ in time $dt$ accelerated to a velocity $u_p$ by a net force $P_1-P_0$ is given by
    • $P_1-P_0={\rho }_0{U}_s{u}_p$
    • how to reduce the equation above?
      • $F=ma$ $P_1-P0={\rho }_0{V}_0\times u_p/dt$ Where the cross-section area is unit. the accelerated part is $u_p$ instead of $U_s-up$ $P_1-P_0={\rho }_0{U}_{s}dt\times u_p/dt$ $P_1-P_0={\rho }_0{U}_s{u}_p$

    • conversation of energy

      • across the shock front is obtained by equating the work done by the shock wave with the sum of the increase of both kinetic and internal energy of the system. Thus
      • $P_1{u}_p=1/2{\rho }_0{U}_s{u}_p^2+{\rho }_0{U}_s(E_1-E_0)$
      • Eliminating $U_s$ and $u_p$ results in the conversation of energy in the popular form known in the literature as the Rankie-Hugoniot relation
      • $E_1-E_0=\frac{1}{2}(V_0-V_1)(P_1+P_0)=\frac{1}{2}(\frac{1}{{\rho }_0}-\frac{1}{{\rho }_1})(P_1+P_0)$
      • The three conversations equations contain a total of 8 parameters-${\rho }_0,{\rho }_1,P_0,P_1,U_s,u_p,E_1,E_0$. If it is assumed that the quantities with zero subscripts are known(i.e., the state of the material ahead of the shock), then three equations with five unknown remain. In order to solve shock problems, we need two more relationships.